В свое время Евклид, основоположник евклидовой геометрии, создал 5 простых утверждение, на которых и основана геометрия в плоскости. И самая последняя аксиома гласила, что через каждую точку вне прямой можно провести лишь одну прямую, параллельную данной .

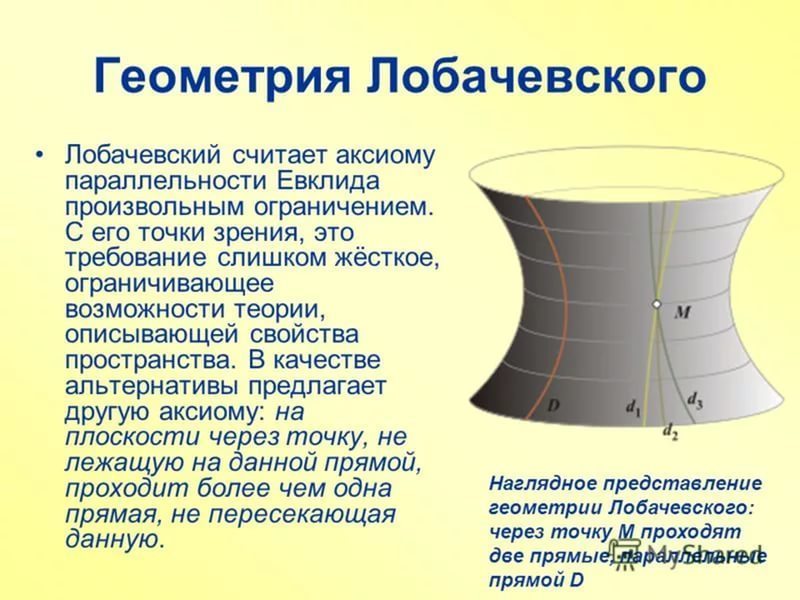
И первый математик, который осмелился возразить данному выражению был Лобачевский. Он, не взирая ни на что, заменил постулат Евклида на свой. И он гласил, что через точку, не лежащую на прямой, можно провести, как минимум, 2 прямые, не пересекающие данную.

Сам Лобачевский создал это утверждение, чтобы найти в ней противоречия и тем самым показать, что Евклид был прав. Однако противоречий все не было. Получалась туфталогия, что сумма углов в треугольнике была меньше 180, а через точку можно на самом деле провести бесконечное множество прямых, параллельных данной, но все это не противоречило. И в конце концов было доказано, что такая система аксиом действительно возможна.