Архимед разработал методы нахождения площадей и объемов, а также методы определения касательных и наибольших и наименьших значений величин, которые он применил для решения проблем статики, гидростатики и теории равновесия плавающих тел. Методы Архимеда легли в основу дифференциального и интегрального исчислений, созданных в XVII в. Архимед нашел все полуправильные многогранники. С помощью конических сечений он решал кубические уравнения вида

х 2 (ах)= b

и проводил полное их исследование.

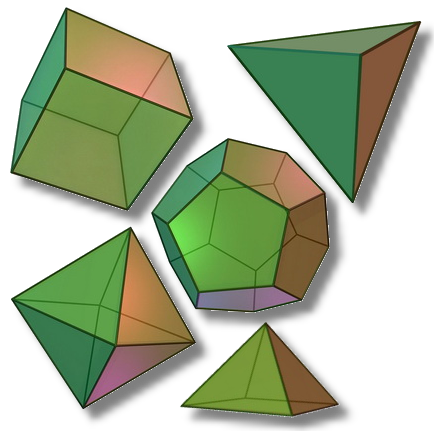
Евклид создал Начала, в которых подвел итог всему предшествующему развитию античной математики. Дедуктивный метод изложения Начал стал образцом для построения математической теории. В Началах систематически изложены геометрия, элементы теории чисел, алгебры, теория отношений и метод исчерпывания. Здесь сформулирован алгоритм Евклида для нахождения наибольшего общего делителя двух чисел, доказано, что произведение чисел ab делится на простое число р тогда и только тогда, когда один из сомножителей делится на р, а также, что простых чисел бесконечно много. В Началах впервые встречается строгий вывод формулы суммы конечного числа членов геометрической прогрессии и показывается, что существует только пять правильных многогранников: куб, тетраэдр, октаэдр, додекаэдр и икосаэдр.